## Group 10 Project 1.2 ### Final presentation Attempt to go to Titan and back with the lowest cost of fuel and as fast as possible. _Fabio Barbero, Krzysztof Cybulski, Cavid Karca, Margarita Naryzhnyaya, Elliot Doe, Michael Balzer_ kutt.it/group10 --- ## Goal of the project - 1 ### Making a Solar System ---- ## Mathematical model ### Phase 1 _Gravitational force_ $$F = G \cdot\frac{m_1\cdot m_2}{d^2}$$ _Euler's method_ $$\vec v_{t+1} = \vec v_t + \vec a_{t}\cdot \Delta t$$ $$\vec x_{t+1} = \vec x_t + \vec v_{t}\cdot \Delta t + \frac{\vec a_{t} \cdot \Delta t}{2}$$ ---- ### Phase 2, 3: Leapfrog | Basic | Kick-drift-kick form | | -------- | -------- | |$$\vec v_{t+\frac{1}{2}}=\vec v_{t-\frac{1}{2}}+\vec a_t\Delta t$$ $$\vec x_{t+1}=\vec x_t+\vec v_{t+\frac{1}{2}}\Delta t$$|$$\vec v_{t+\frac{1}{2}} = \vec v_t + \vec a_t \frac{\Delta t}{2}$$ $$\vec x_{t+1} = \vec x_t + \vec v_{t + \frac{1}{2}}\Delta t$$ $$\vec v_{t+1} = \vec v_{t + \frac{1}{2}} + \vec a_{t+1} \frac{\Delta t}{2}$$| ---- ### Phase 2, 3: Verlet $$\vec x_{n+1}=2\cdot\vec x_{n-1}+\vec a \cdot \Delta t^2$$ ---- ### Energy drift  ---- ### 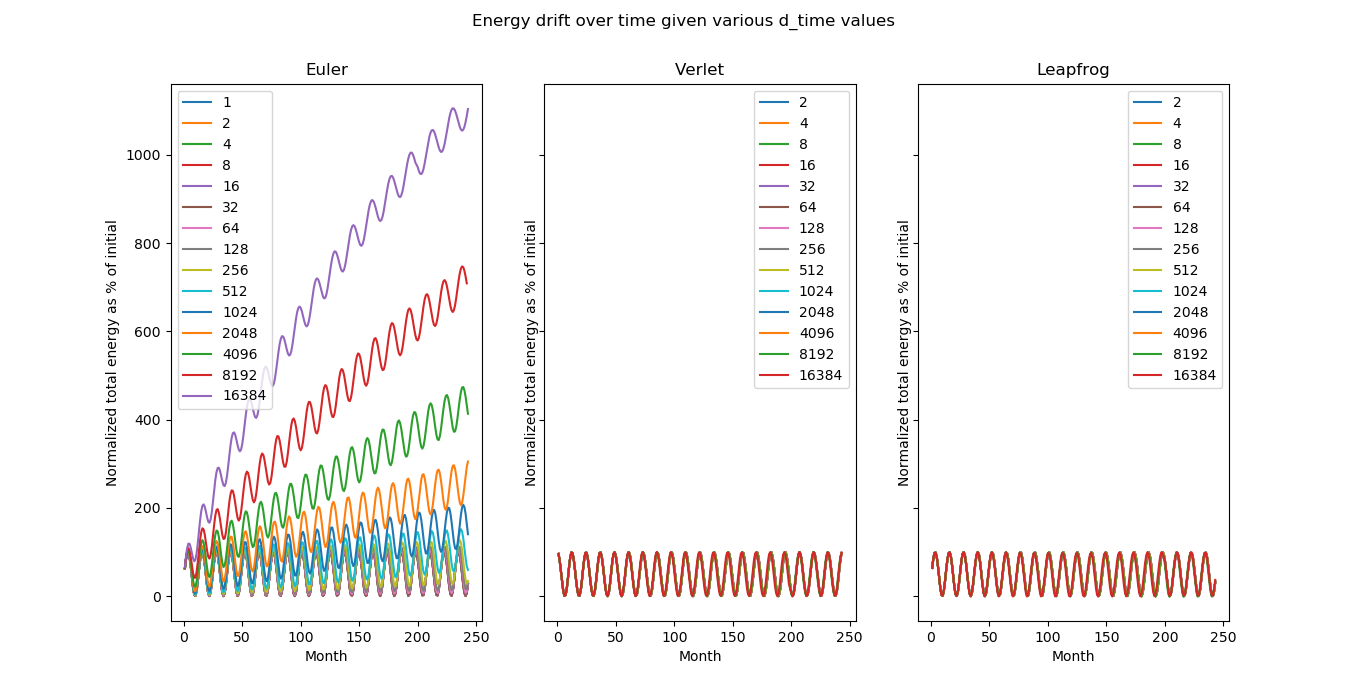Runtime of Leapfrog, Euler and Verlet methods  ---- ## 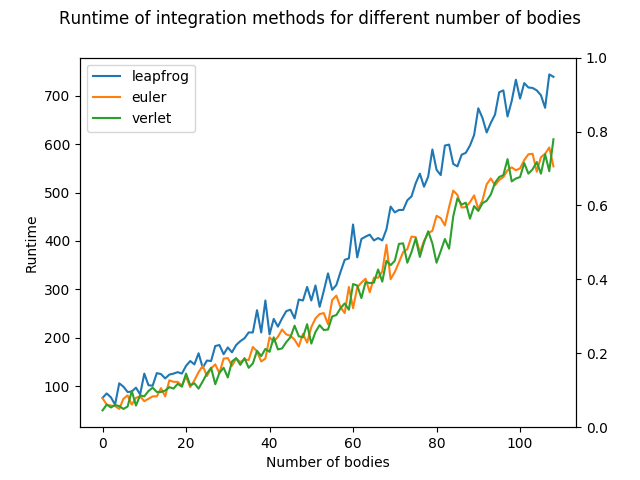Precomputing positions <!-- .slide: data-background="/uploads/sapproximator1.gif"-->  ---- ## Visualisation 2D  ---- ## Visualisation 3D  --- ## Central body simulation - Rotation - Atmosphere - Air resistance ---- ## Rotation - Planets orbit the sun with a certain speed and on rotate around their axis - Useful to know the location where the landing should take place - Only taken into account when landing on celestial bodies ---- ## Rotation  ---- ## Atmosphere ### 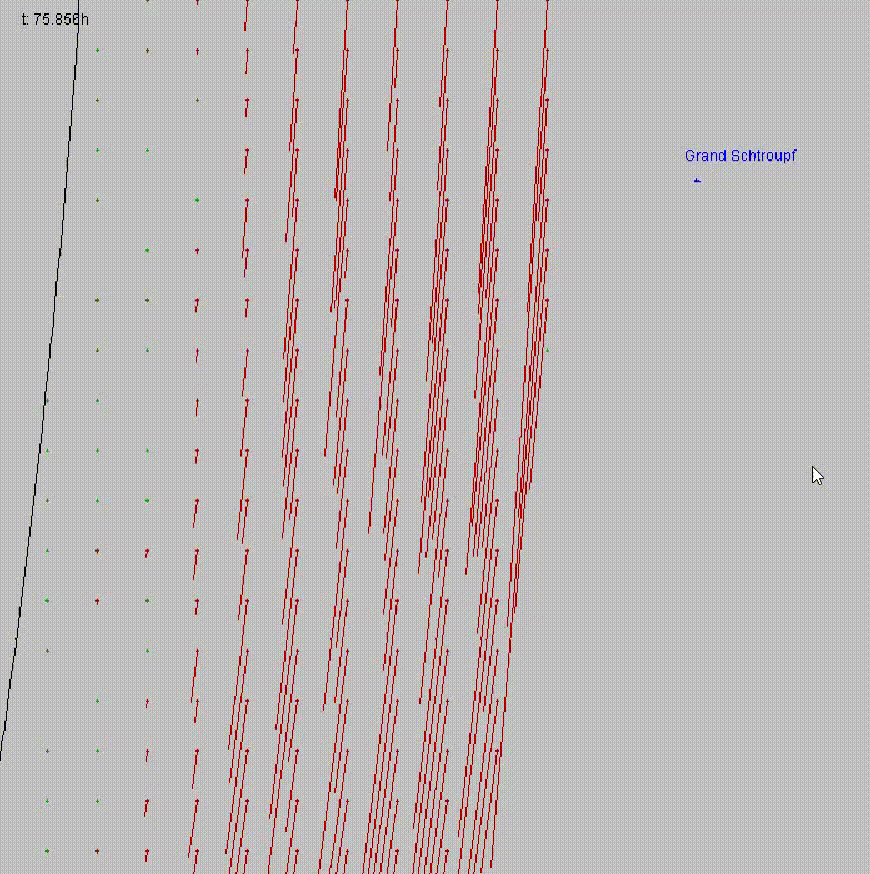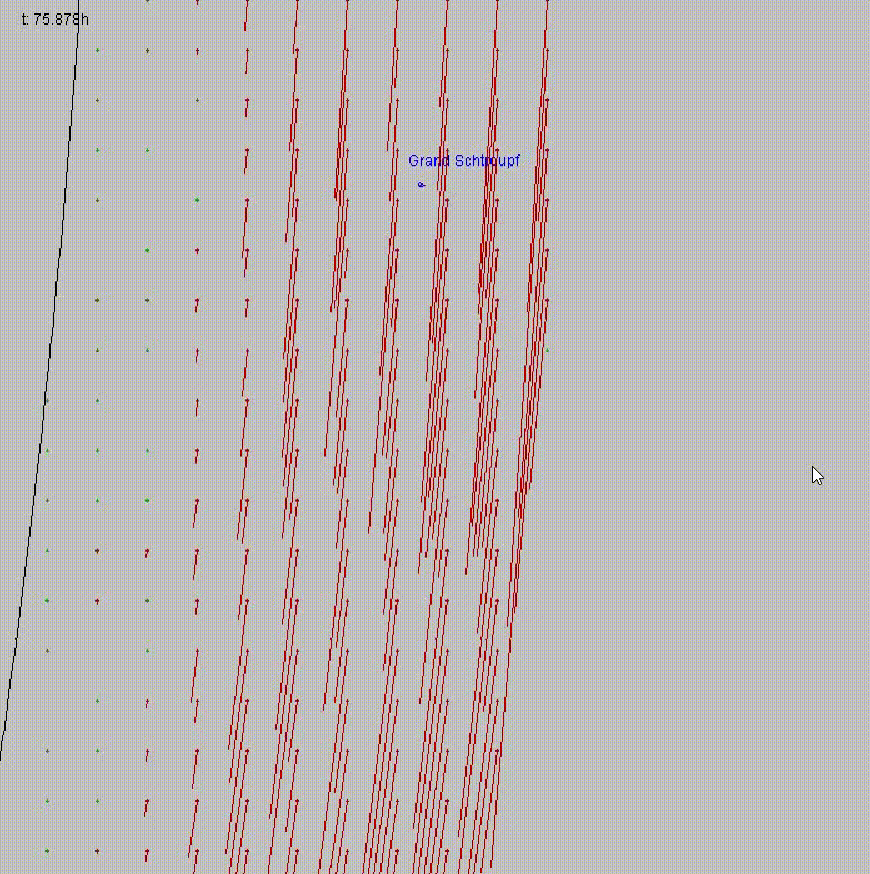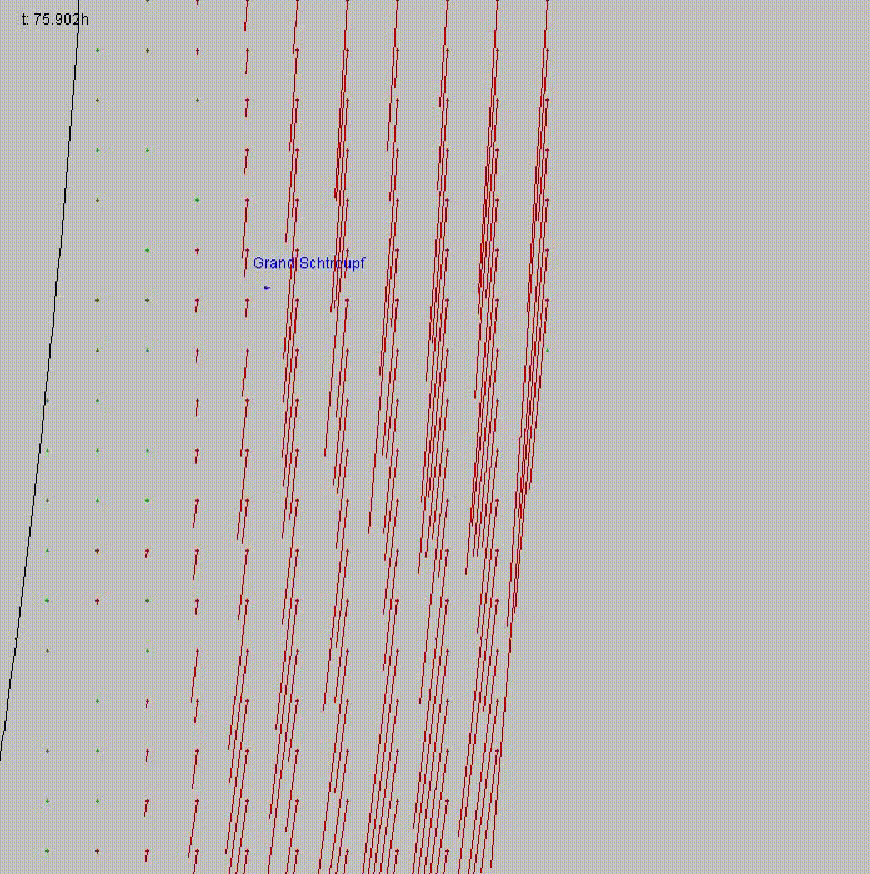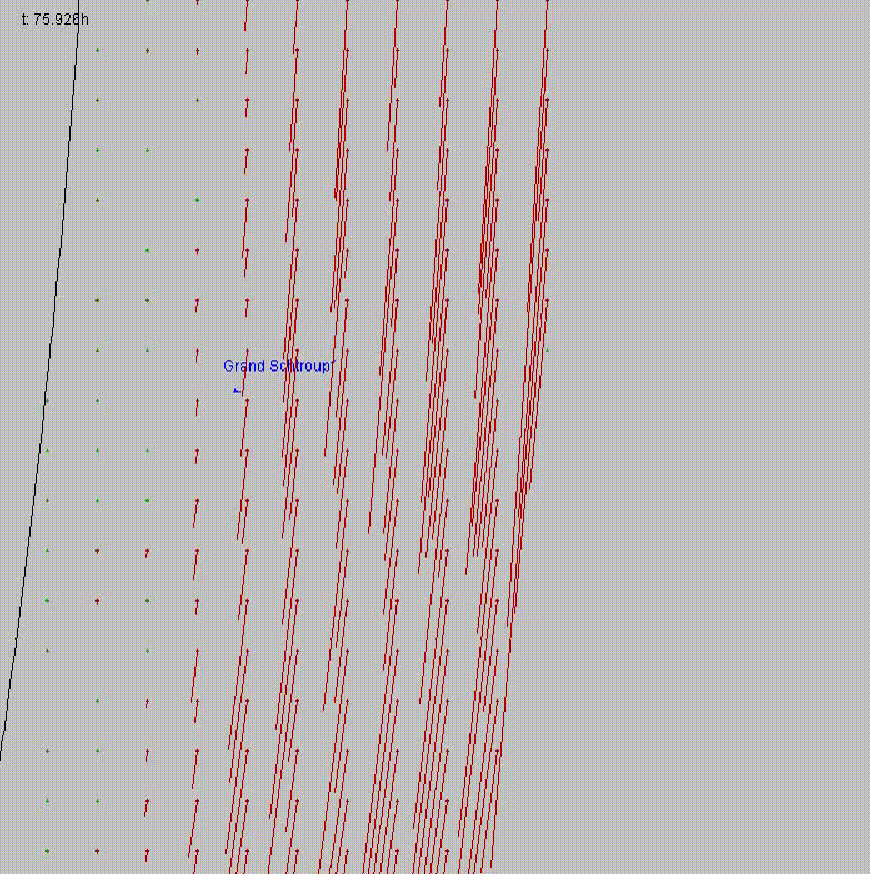Wind on Titan - Wind load formula: $$A \cdot p \cdot v^2 \cdot 0.5 \cdot C$$ Where $A$ is the projected area $p$ is the pressure $v$ is the velocity of the wind $C$ is the drag coefficient ---- ## Wind function  ---- ## 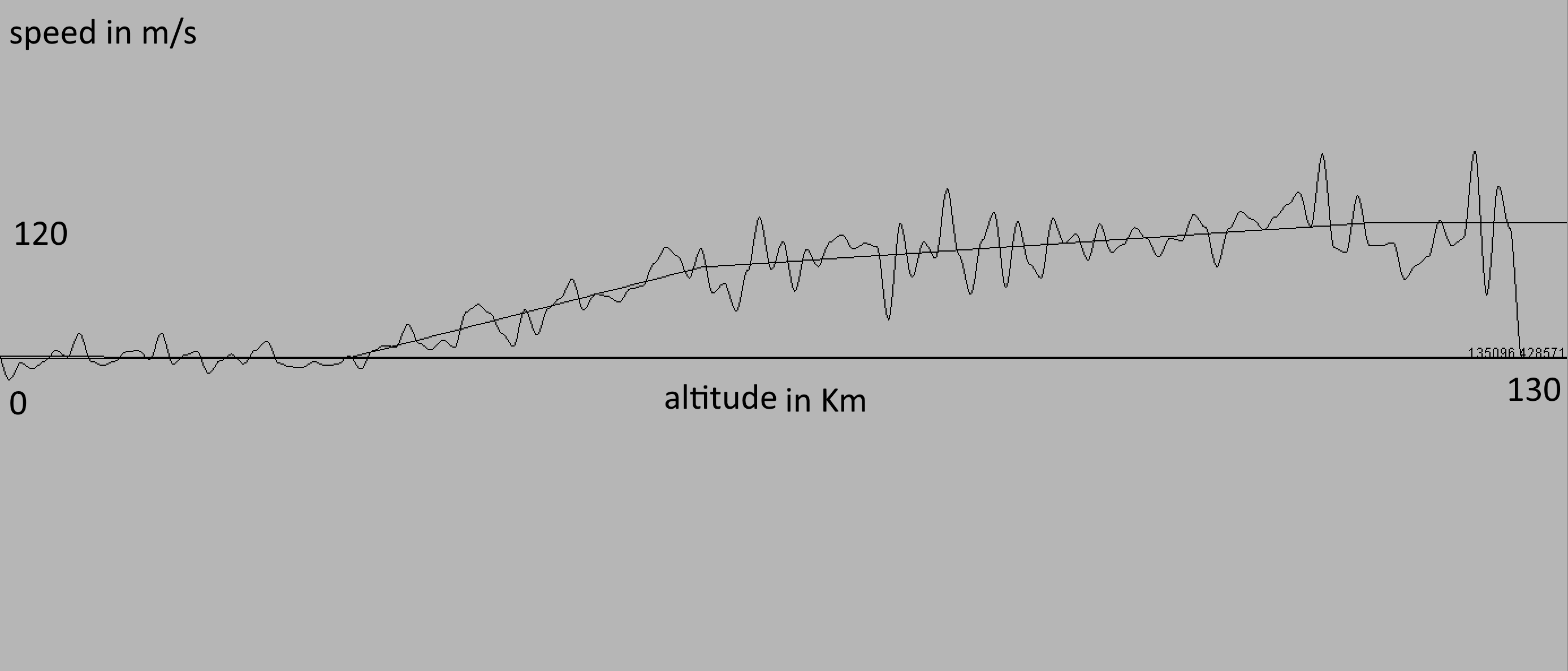Wind demo  ---- ## Air resistance Air resistance: $$F = 0.5 \cdot p(a) \cdot C \cdot A \cdot v^2$$ $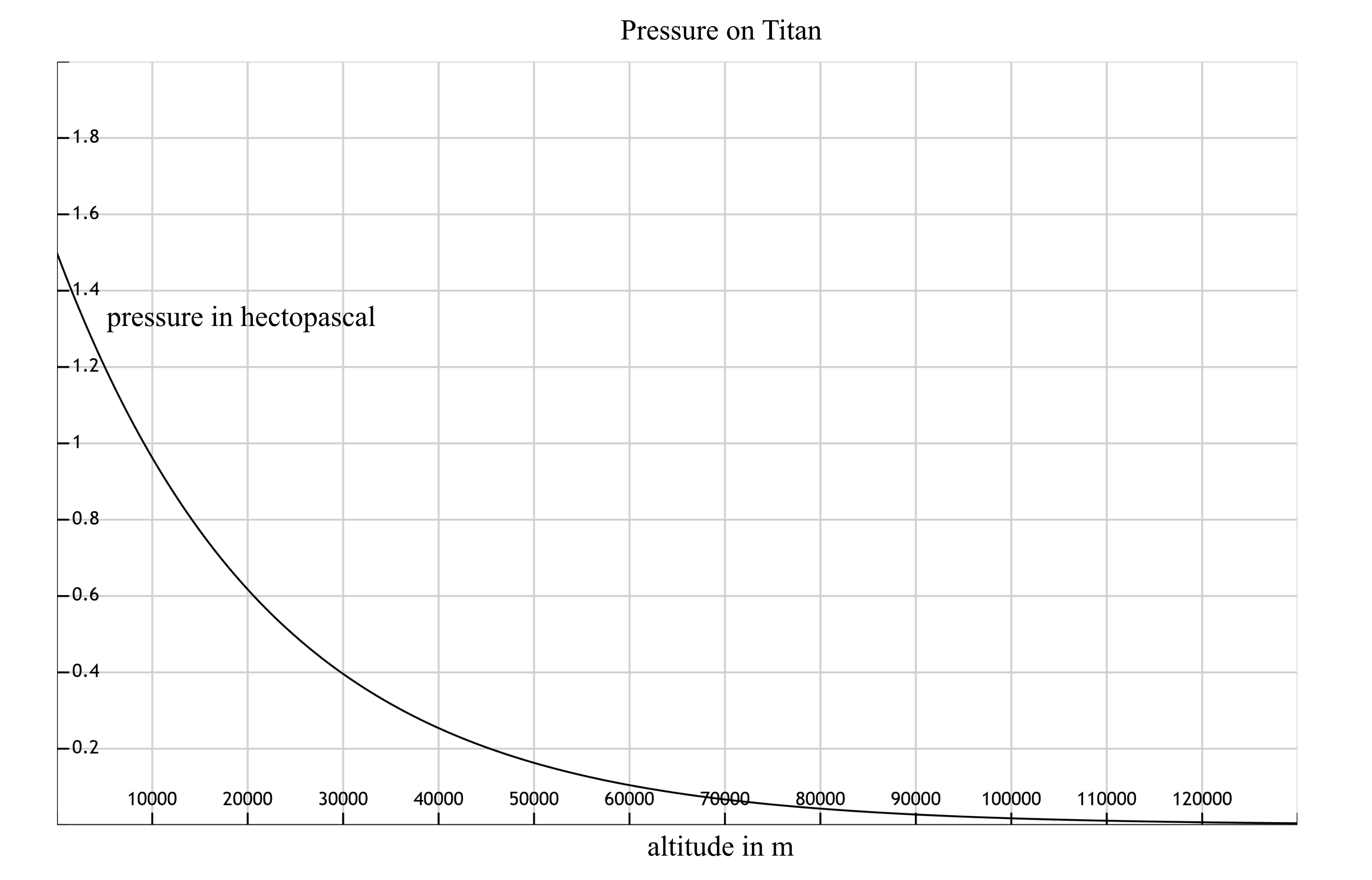p(a)$ pressure in terms of altitude $C$ drag coefficient $A$ area spacecraft $v$ speed of spacecraft ---- ### Pressure function  --- ## Space voyage - consists of different spacecraft phases - combined they represent a space mission ---- ## 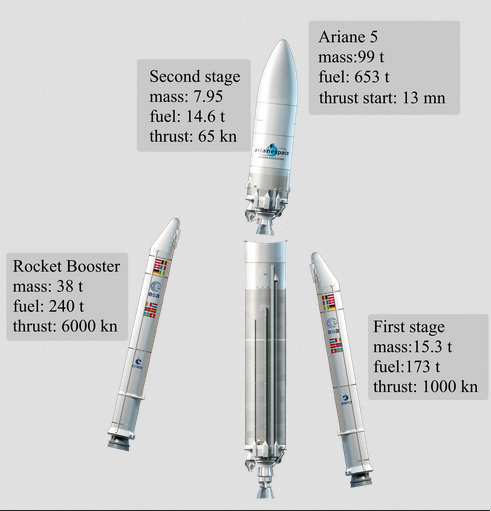Spacecraft  ---- ## Spacecraft  --- ## 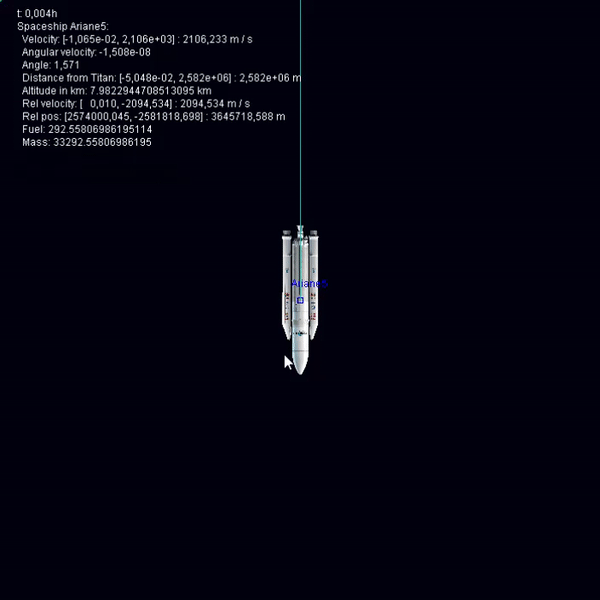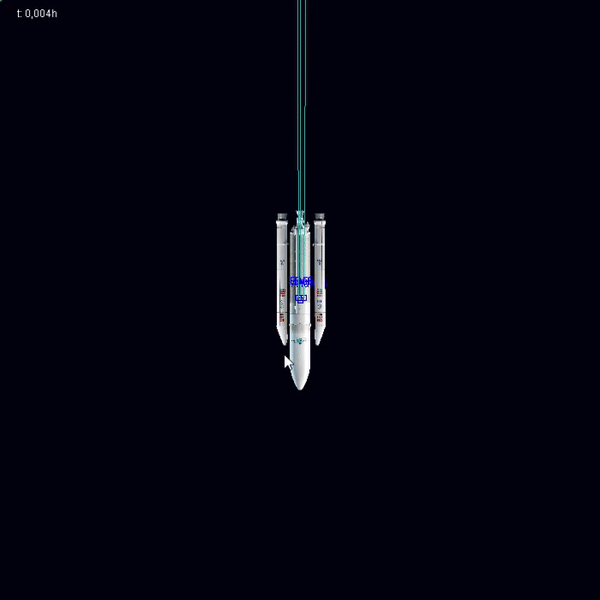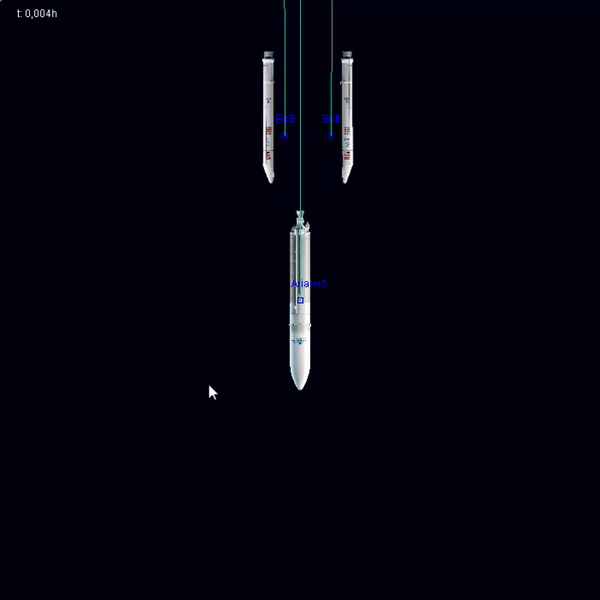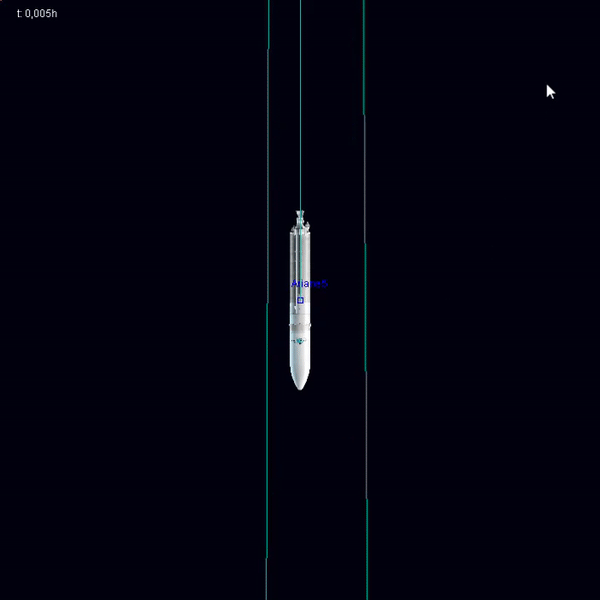Switching from 2D to 3D --- ## Launching from Earth - using a multistage Rocket to enter stable orbit - simple feedback controller - adjusting angle depending on altitude ---- ## Hohmann transfer $v_{p} = \sqrt{GM\left(\frac{2}{r} - \frac{1}{a} \right)}$  ---- ## Interplanetary travel  --- ## Landing on Titan ---- ### Open-loop Controller A controller that only gets time as the input. - This is doable with constant gravity. Realistic gravity makes precomputation significantly more complex. - Simple implementation with constant gravity. 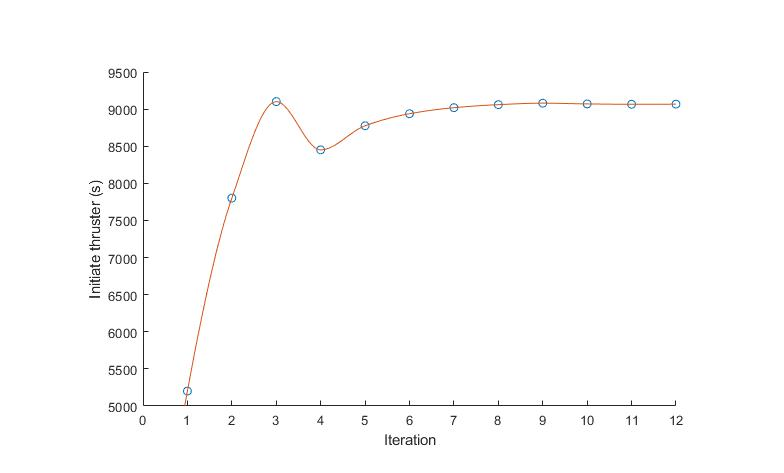---- ### Open-Loop controller pre-computation  --- ### Closed-loop Controller - AKA feedback controller - Used to determine the thrust based on the current position and velocity. - PID-Controller ---- ### PID-Controller - Proportional - Integral - Derivative Combined, they form the PID-controller. ---- ### Proportional control $$P_{out}=K_p\cdot e(t)$$ $P_{out}$ = Proportional correction $K_p$ = Adjustable constant for proportional controller $e$ = error $t$ = time ---- ### Integral control $$I_{out} = K_i\int _{0}^{t} e(\tau)\, d\tau$$ $I_{out}$ = Integral correction $K_i$ = Adjustable constant for integral controller $\tau$ = Variable of the integral ---- ### Derivative control $$D_{out} = K_d\cdot \frac{de(t)}{dt}$$ $D_{out}$ = Derivative correction $K_d$ = Adjustable constant for derivative controller $\tau$ = Variable of the integral --- ## Back to Earth - Similar procedure, but reversed --- ## Fuel - Kerosene (or RP-1, rocket propellant 1) is used as fuel for the spaceship. - Kerosene is a bipropellant. - Liquid Oxygen (LOX) used as oxidizer for the fuel. ---- ### Mass flow rate Mdot is the mass flow rate of the spacecraft. $$\dot{m} = r\cdot V\cdot A$$ $r$ = Density of the fuel $V$ = Velocity of the fuel $A$ = Area of the nozzle ---- ### Mass flow rate $$\boldsymbol {F = \dot{m}\cdot V_e + (P_e - P_0)\cdot A_e}$$ $F$ = Thrust in N $\dot{m}$ = Mass-flow rate in kg/s $V_e$ = Exit velocity $P_e$ = Exit pressure $p_0$ = free stream pressure $A_e$ = Exit area --- ## Fuel use | Real Ariane 5 | Modified | | -------- | -------- | ||| --- ### 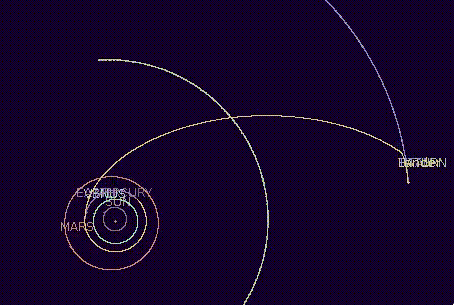Landing results  ---- ### 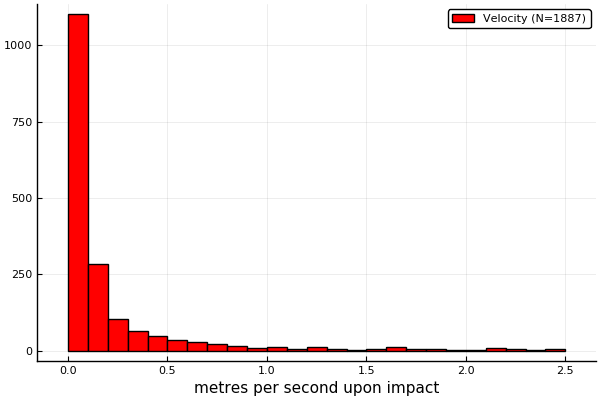Landing results  --- # 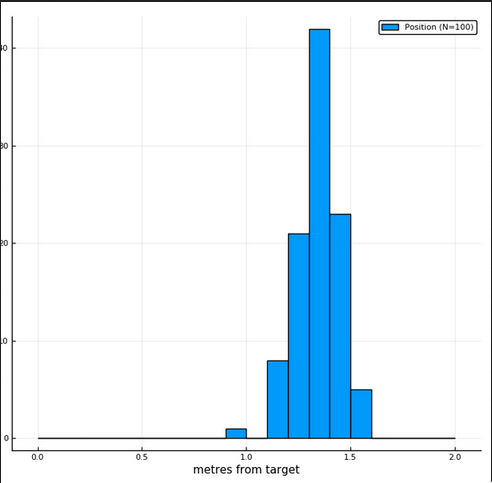Conclusion ---- # Questions?